ANSYS
Sauvegarde
et lecture d’un travail :
Spécification
des propriétés du matériau
Introduction
ANSYS est un logiciel de modélisation d’élément fini utilisé pour la résolution numérique d’une grande variété de problèmes mécaniques. Ces problèmes incluent : les phénomènes structuraux statiques et dynamiques (linéaire et non linéaire), thermiques et acoustiques.
En général, une solution par modèle d'élément finie peut être classée en trois étapes :
- Prétraitement (définition du problème) :
- Définition de la géométrie "keypoints/lines/areas/volumes"
- Définition du type
d'élément et les propriétés du matériau
- Solution (assigner des
charges et des contraintes) : dans cette partie, nous indiquons les charges (point
ou pression), des contraintes (de translation et de rotation) et nous
résolvons finalement l'ensemble des équations.
- Post-traitement (visualisation des résultats) : dans cette étape on peut visualiser :
- Les déplacements nodaux
- Les forces et les moments
- Les diagrammes de contour de tension
Démarrer Ansys :
Avant tout, assurez vous de sauvegarder régulièrement votre travail.
Aller dans démarrer à Tous les programmes à Ansys 9.0 à Ansys.
Ansys est composé de deux fenêtres, la fenêtre principale (Main window) et la fenêtre de sortie (Output window).
Output window : Cette fenêtre affiche les messages de sortie du programme.
La fenêtre principale est divisée en 5 sous-menus :

Utility menu : ce menu de service contient les fonctions qui sont disponibles dans toute la session Ansys, telle que les commandes d’édition et de graphisme etc.….
Input line : La ligne d'entrée affiche les messages de sortie et vous permet de saisir des commandes directement.
Toolbar : Contient les icônes d’exécution des commandes d’Ansys.
Main menu : Le menu principal contient les fonctions primaires d'Ansys, le prétraitement, la résolution, le post-traitement général et l’optimisation.
Graphics window : C’est la fenêtre où les graphiques sont affichés.
Sauvegarde et lecture d’un travail :
Il est recommandé de sauvegarder régulièrement votre travail pendant la séance de TP. De cette façon, si vous faites quelques erreurs plus tard, vous pourrez au moins reprendre votre travail sur la base des fichiers sauvegardés.
Pour sauvegarder votre modèle, aller sur Utility Menu Bar -> File -> Save As votre_travail.db. Votre modèle sera ainsi archivé dans un dossier appelé votre_travail.db.
Pour relire votre travail lors d’une nouvelle utilisation de ANSYS aller sur Utitily Menu -> File -> Resume from et indiquer le nom de votre projet, par exemple votre_travail.db.
Impression des résultats
Pour sauvegarder rapidement un graphique ou le résultat sous ANSYS choisisser:
- 'Utility menu bar'/'PlotCtrls'/'Hard
Copy ...'.
- Selectioner soit
'Graphics window', 'Monochrome', 'Reverse Video', 'Landscape'
- 'Save to:'.
- Donner un nom à votre figure.
- 'OK'
Votre image est ainsi sauvegardée sous forme d’un fichier Postscript que vous pouvez imprimer.
Tutorial
Ce tutorial est une illustration des fonctionnalités d’ANSYS.
Considérer une plaque carrée d’épaisseur uniforme avec un trou circulaire (ses dimensions sont représentées sur la figure ci-dessous). L'épaisseur de la plaque est de 1 millimètre. Le module de Young E = 10 7 MPa et le coefficient de Poisson nu = 0,3. Une pression uniforme p = 1 M·Pa agit sur la surface du trou. Nous nous proposons de calculer les contraintes et leurs déplacements en utilisant ANSYS.

Mise en route
- Créer un répertoire appelé plaque pour la sauvegarde des fichiers d’Ansys.
- Démarrer Ansys : démarrer > Tous les programmes > Ansys 9.0 > Ansys
Dans la fenêtre affichée indiquer le chemin du répertoire crée :
- File > Save as… indiquer le répertoire de sauvegarde ainsi que le nom du fichier.
Indiquer les préférences
- Aller sur : Main Menu > Preferences
Sélectionner Structural et cliquer ensuite sur OK.

Saisie des paramètres
- Aller sur : Utility Menu > Parameters > Scalar Parameters
- Saisir le paramètre a=10e-3 puis cliquer sur Accept.
- De même, entrer les autres valeurs en cliquant sur Accept après chaque saisie.
r=7e-3
p=1e6
E=1e13
nu=0.3
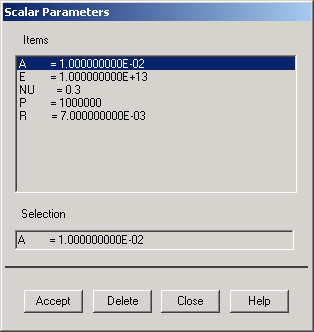
Fermer la fenêtre en cliquant sur Close.
Spécification des constantes
- Pour spécifier les différentes constantes aller sur : Main Menu > Preprocessor> Element Type > Add/Edit/Delete > Add...
- Sélectionner Structural Solid dans la partie gauche de la fenêtre et Quad 4 node 42 dans la partie droite.

- Cliquer sur OK pour avoir la fenêtre suivante.

Cette étape nous permet de
choisir le type de modèle à utiliser,
PLANE42 est un plan défini par quatre
points et à deux degrés de liberté.
- Pour Valider les constantes de notre modèle aller sur : Real Constants > Add/Edit/Delete > Add
- Cliquer sur OK
Vous devriez obtenir un message disant "Please check and change keyopt setting for element PLANE42 before proceeding." Fermer alors le message et sauvegarder votre travail.
Spécification des propriétés du matériau
- Main Menu > Preprocessor >Material Props > Material Models ....
Double clique sur Structural, Linear, Elastic, et Isotropic

- Nous emploierons les variables définis précédemment pour indiquer les propriétés du matériau. Entrer E pour le module de Young EX et nu pour le coefficient de Poisson PRXY.
- Cliquer sur OK et sauvegarder votre travail.
Géométrie
Comme toutes les propriétés du matériau sont symétriques nous allons faire le calcul sur un quart de notre plaque, nous généraliserons par la suite le résultat au système entier. Nous choisissons l’origine du système au centre de la plaque.
-Pour dessiner le carré représentant la plaque, aller sur : Main Menu > Preprocessor > Modeling >Create > Areas >Rectangle > By Dimensions

X1 et X2 sont les coordonnées de l’arête gauche et l’arête droite du carré, Y1 et Y2 sont les coordonnées de l’arête inférieur et l’arête supérieure du carré.
- Entrer les valeurs X2 = Y2 = a et X1 = Y1 = 0.
- Cliquer sur OK
- Pour Créer un trou dans notre plaque aller sur : Main Menu > Preprocessor > Modeling > Create > Areas > Circle > Partial Annulus
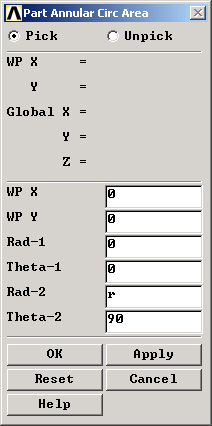
WP X et WP Y sont les coordonnées du centre du quart de cercle qu’on veut créer.
Rad-1 est le rayon du quart de cercle. Saisir 0 pour Rad-1 (pour avoir un cercle plein).
Rad-2 est le rayon
(externe) du cercle. Saisir r pour Rad-2.
Theta-1 et Theta-2 sont les angles qui définssent le cercle. Saisir 0 pour Theta-1 et 90 pour Theta-2. Cliquer sur OK
- Pour substituer le quart de cercle crée sur notre modèle aller sur : Main Menu > Preprocessor >Modeling > Operate > Booleans > Subtract > Areas
Dans la fenêtre d'entrée, ANSYS vous indique "pick or enter base areas from which to subtract". Tout en
maintenant le bouton gauche de la souris, déplacer le curseur au-dessus du
modèle jusqu'à ce que la plaque change
de couleur. Cliquer sur OK.

ANSYS vous indique maintenant "pick or enter areas to be subtracted". Indiquer alors la partie à enlever du modèle. Cliquer sur OK.

Le résultat final ressemble au modèle de la figure ci-dessus :

Sauvegarder votre travail.
Maillage
Dans ce qui suit nous allons indiquer des paramètre technique pour la résolution des équations différentielles utilisées dans la simulation par éléments finis.
Main Menu > Preprocessor > Meshing > MeshTool

Vérifier que Global est sélectionné dans Element Attributes, cliquer sur set :
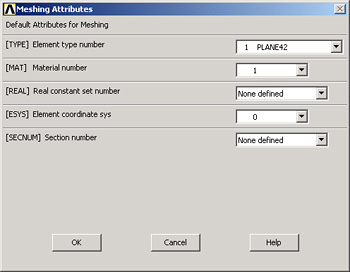
Sélectionner les paramètres indiqués sur la figure ci-dessus.

Aller maintenant sur Mesh Areas et sélectionner la surface à mailler, valider par Ok.

- Sauvegarder votre travail.
Conditions aux limites
Dans cette partie nous configurons les conditions aux limites, la distribution des contraintes et des charges au niveau des bords.
- Aller sur : Main Menu > Preprocessor > Loads > Define Loads > Apply > Structural > Displacement > Symmetry B.C. > On Lines
- Cliquer sur la ligne de gauche et celle du bas pour sélectionner les bords avec lesquels nous allons générer le reste de la plaque.

- Pour appliquer la pression au niveau du trou aller sur : Main Menu > Preprocessor > Loads > Define Loads > Apply > Structural > Pressure > On Lines
- Entrer la valeur p et cliquer ensuite sur le demi cercle qui défini le trou et valider par OK. Vous aurez alors un modèle qui ressemble à celui de la figure ci-dessous

- Sauvegarder votre travail.
Résolution du problème
- Aller sur : Main Menu > Solution > Solve > Current LS et valider par Ok.

Post-traitement
Dans cette partie nous allons visualiser les résultats de notre simulation. Dans un premier lieu nous allons observer la déformation de notre plaque :
- Aller sur : Main Menu > General Postproc > Plot Results > Deformed Shape, sélectioner Def + undeformed et cliquer sur Ok
Ceci représente la structure initiale et déformé. La déformation maximum DMX est de 0.232E-08m.
Pour avoir une animation de cette déformation vous aller sur : Utility Menu > PlotCtrls > Animate > Deformed Shape...
-
Sélectionner Def + undeformed et
cliquer sur Ok.
Pour avoir la distribution des contraintes en contours couleurs aller sur : Main Menu > General Postproc > Plot results > Contour Plot > Nodal Solu
-
Sélectionner Stress
dans le menu gauche et von Mises SEQV dans le menu droit.
Pour avoir une animation de la déformation en contours couleurs aller sur : tility Menu > PlotCtrls > Animate > Mode Shape...
-
Sélectionner Stress
dans le menu gauche et von Mises SEQV dans le menu droit.
Pour sauvegarder en image les résultats graphique aller sur : Menu > PlotCtrls > Capture image….
Travail supplémentaire
-
Le tableau ci-dessous représente le module de Young de
quelques matériaux. Pour chaque matériau listé dans le tableau tracer la variation
du déplacement maximum (DMX), en utilisant un tableur, en fonction de la
pression appliquée sur le trou. En considère que le coefficient de poisson vaut
0.3 pour tous les matériaux et que la limite élastique n’est pas dépassée.
- Classer ces matériaux en fonction de leurs rigidités, commenter.
Module de Young
Le physicien anglais Thomas Young avait remarqué que le rapport entre la contrainte de traction appliquée à un matériau et la déformation qui en résulte (un allongement relatif) est constant, tant que cette déformation reste petite et que la limite d'élasticité du matériau n'est pas atteinte. Cette constante est le module d'Young ou module d'élasticité longitudinal. La loi d'élasticité est la loi de Hooke :
![]()
où :
- σ est la contrainte (pression)
- E est le module d'Young,
- ![]() est
la déformation.
est
la déformation.
Le module d'Young est la contrainte mécanique qui engendrerait un allongement de 100 % de la longueur initiale d'un matériau (il doublerait donc cette longueur), si on pouvait l'appliquer réellement : dans les faits, le matériau se déforme de façon permanente, ou se rompt, bien avant que cette valeur soit atteinte.
Limite d'élasticité
La limite d'élasticité est la contrainte à partir de laquelle un matériau commence à se déformer de manière permanente. Elle se mesure ou se vérifie habituellement à l'aide d'un essai de traction. Elle s'exprime en pascal (Pa). On peut la noter :
- σy en raison du terme anglais yield strength
- Re
- σ0,2
- Rp0,2
|
Matériaux |
Module de Young (MPa) |
Limite d’élasticité
(MPa) |
|
PVC |
100 |
48 |
|
Fer |
196 000 |
50 |
|
Carbure de Silicium (SiC) |
450 000 |
10 000 |
|
Diamant |
1 000 000 |
50 000 |
|
Verre |
69 000 |
3600 |
|
Polyéthylène |
700 |
20 |
